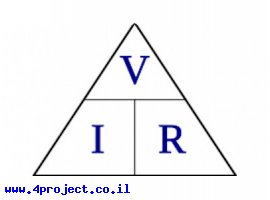
מעגלים פשוטים (אלה שיש בהם רק כמה רכיבים בודדים) בדרך כלל די ברורים להבנת המתחילים. אבל, הדברים יכולים להסתבך כשמוסיפים עוד ועוד רכיבים לחגיגה. לאן זורם הזרם? מה המתח עושה? האם אפשר לפשט את זה כדי להקל על ההבנה? לא להיבהל, בהמשך נסביר את הכל.
במדריך זה קודם נסביר על ההבדל בין מעגלים טוריים ומעגלים מקביליים. לצורך כך נשתמש במעגלים עם רכיבים הבסיסים ביותר, נגדים וסוללות, כדי להראות את ההבדלים בין שתי צורות החיבור. אחרי זה נחקור מה קורה במעגלים טוריים ומקביליים כשמשלבים בין רכיבים שונים, כמו קבלים וסלילים.
מדריך זה מכסה את הנושאים הבאים:
- איך נראים חיבורים במעגלים טוריים ומקביליים
- איך רכיבים פסיביים מתנהגים בצורות חיבור אלה
- איך מקור מתח משפיע על הרכיבים הפסיביים בחיבורים אלה
מדריכים מומלצים
רצוי לעבור על המדריכים הבאים המסבירים על רכיבים בסיסיים לפני שתתחילו לבנות מעגלים המופיעים במדריך זה:- מה זה חשמל?
- מתח, זרם, התנגדות וחוק אוהם
- מהו מעגל?
- קבלים
- TODO: Inductors
- נגדים
- איך משתמשים במטריצה
- איך משתמשים ברב-מודד
מעגלים טוריים
צמתים/חיבורים וכיוון זרימת הזרם
לפני שצוללים לפרטים, בואו נבין קודם מה זה צומת (node). לא משהו מיוחד, זה פשוט ייצוג של חיבור חשמלי בין 2 או יותר רכיבים. כשמעגל ממומש בשרטוט חשמלי, הצמתים מייצגים את החוטים בין הרכיבים.דוגמה של שרטוט עם 4 צמתים המצויירים בצבעים שונים.
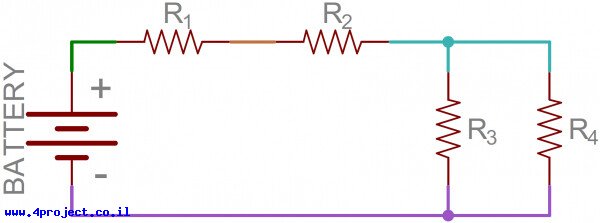
זוהי חצי דרך להבנת ההבדל בין חיבור טורי ומקבילי. אנחנו צריכים גם להבין איך הזרם זורם דרך המעגל. זרם זורם ממתח גבוה למתח נמוך במעגל. חלק מסוים של הזרם יזרום דרך כל המסלולים של המעגל כדי להגיע למתח הנמוך (בדרך כלל מכונה כאדמה). אם נקח את המעגל הקודם כדוגמה, כך הזרם יזרום מהצד החיובי של הסוללה לצד השלילי. הזרם מצויין עם החצים בצבעים כחול, כתום וורוד:
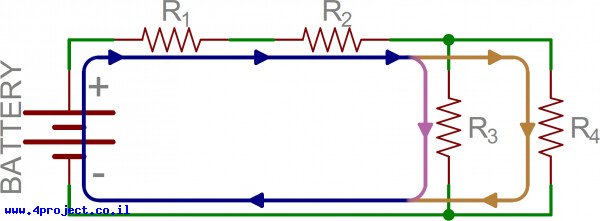
שימו לב שבצמתים מסוימים (כמו בין R1 ו-R2) הזרם שנכנס הוא אותו הזרם שיוצא. בצמתים אחרים (הצומת המשולש בין R2, R3 ו-R4), הזרם העיקרי (הכחול) מתפצל לשני זרמים שונים (כתום וורוד). וזהו ההבדל בין טורי למקבילי!
הגדרה של מעגל טורי
שני רכיבים מחוברים בטור אם יש להם צומת/חיבור משותף ועובר דרכם אותו הזרם. הנה דוגמה של מעגל עם 3 נגדים שמחוברים בטור: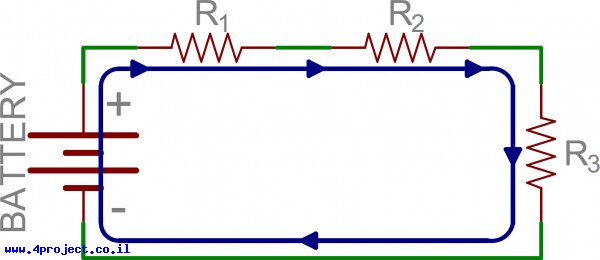
במעגל כזה לזרם יש רק דרך אחת לזרום. מתחילים בצד החיובי של הסוללה, עוברים דרך נגד R1, משם ישירות ל-R2, משם ל-R3 ובחזרה לצד השלילי של הסוללה. שימו לב שלזרם יש רק מסלול אחד שהוא יכול לעבור. רכיבים אלה מחוברים בטור.
מעגלים מקביליים
הגדרה של מעגל מקבילי
אם רכיבים משתתפים ב-2 צמתים, אז הם מחוברים במקביל. הנה דוגמה של מעגל עם 3 נגדים שמחוברים במקביל לסוללה: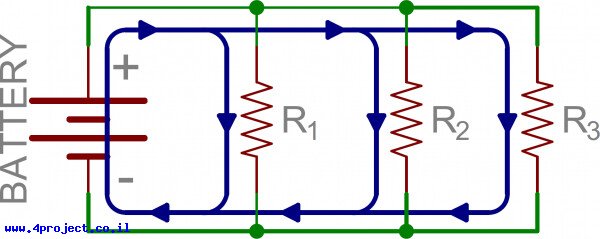
הזרם זורם מהצד החיובי של הסוללה ל-R1… וגם R2, וגם R3. הצומת שמחבר את הסוללה לנגד R1 מחוברת גם לנגדים אחרים. הצד השני של הנגדים מחובר באותה הצורה לצד השלילי של הסוללה. לזרם יש 3 מסלולים שונים שהוא יכול לעבור לפני שהוא חוזר לסוללה. נגדים שמחוברים בצורה זו הם נגדים מקביליים.
כלל אצבע: לרכיבים המחוברים בטור יש את אותו הזרם שעובר דרכם. לרכיבים המחוברים במקביל יש את אותו מפל המתח. בטור - זרם, במקביל - מתח.
שילוב בין מעגלים טוריים ומקביליים
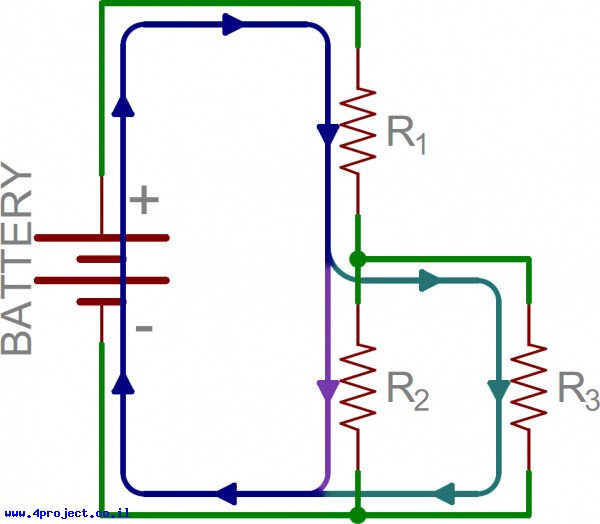
אפשר גם לערבב את שתי צורות החיבור. בתמונה הבאה אנחנו שוב רואים 3 נגדים וסוללה. מהצד החיובי של הסוללה הזרם קודם פוגש את הנגד R1, אבל בצידו השני של R1 החיבור מתפצל והזרם יכול לזרום גם ל-R2 וגם ל-R3. הזרם עובר דרך R2 ו-R3 ואחרי זה שוב מתלכד וזורם לצד השלילי של הסוללה.בדוגמה זו הנגדים R2 ו-R3 מקבילים אחד לשני, ונגד R1 מחובר בטור לשילוב המקבילי של R2 ו-R3.
חישוב התנגדות במעגל טורי
הגענו לנושאים שיהיו קצת יותר פרקטיים עבורכם. כשמחברים את הנגדים בצורות אלה, בטור או במקביל, אנחנו משנים את הדרך שהזרם זורם דרכם. לדוגמה, אם יש לנו 10V על פני נגד של 10kΩ, חוק אוהם אומר שיהיה לנו זרם של 1mA.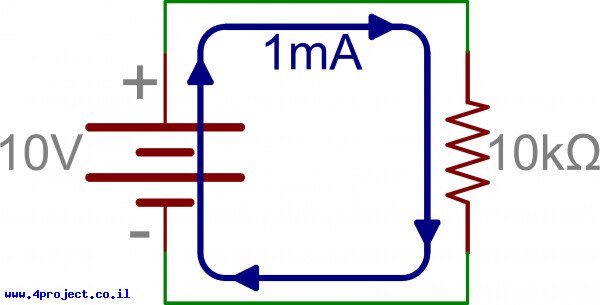
אם נחבר עוד נגד של 10kΩ בטור לנגד הקיים בלי שינוי באספקת המתח, נקטין את הזרם בחצי מכיוון שההתנגדות הוכפלה.
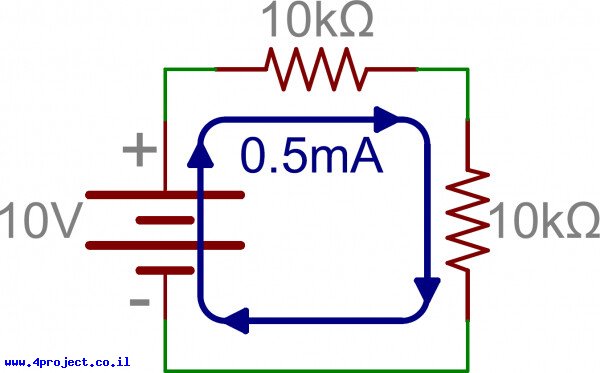
במילים אחרות, לזרם עדיין יש רק מסלול אחד לזרום דרכו ואנחנו גרמנו למסלול הזה להיות קשה יותר לזרימה. כמה קשה? פי שתיים. 10kΩ + 10kΩ = 20kΩ. וזו הדרך בה אנחנו מחשבים את ההתנגדות של הנגדים המחוברים בטור - פשוט מחברים את הערכים שלהם.
הנוסחה הכללית יותר תהיה: ההתנגדות הכוללת של N נגדים בטור = סכום ההתנגדויות של כל N הנגדים.
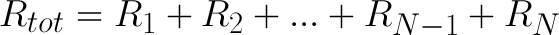
חישוב התנגדות במעגל מקבילי
מה לגבי הנגדים במקביל? זה קצת יותר מסובך, אבל לא יותר מדי. נמשיך מהדוגמה בה מקור מתח של 10V מחובר לנגד של 10kΩ, אבל נחבר לו עוד נגד של 10kΩ במקביל. עכשיו לזרם יש שני מסלולים דרכם הוא יכול לזרום. מקור המתח לא השתנה, חוק אוהם אומר שהנגד הראשון עדיין יצרוך זרם של 1mA. אבל כך גם הנגד השני, כך שעכשיו יש לנו סה"כ 2mA שיוצאים מהספק, כפול מה-1mA שהיו קודם. מכך אפשר להסיק שצמצמנו את ההתנגדות בחצי.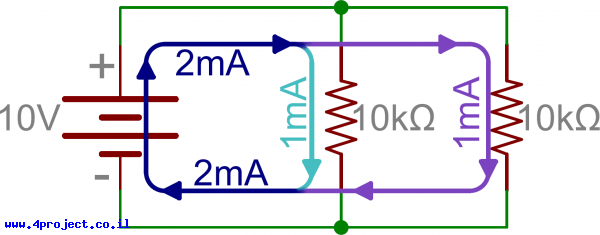
אפשר להכריז ש: 10kΩ || 10kΩ = 5kΩ (הסימון "||" מציין "במקביל ל-"). אבל לא תמיד יהיו לנו שני נגדים עם ערכים זהים… מה אז?
הנוסחה להוספת כמות מסוימת של נגדים במקביל היא:
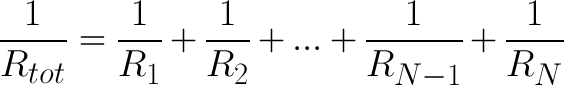
אפשר להשתמש בנוסחה מצומצמת כשיש לנו רק שני נגדים:
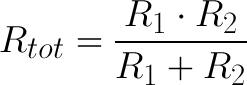
גם אם הנוסחה מתאימה רק לשני נגדים, עדיין נוכל להשתמש בה לחישוב ההתנגדות של יותר משני נגדים שמחוברים במקביל. מחשבים את התוצאה של R1 || R2 ומשתמשים בה בחישוב עם הנגד השלישי שמחובר במקביל. עם הרבה נגדים הנוסחה הארוכה יותר דורשת פחות מאמץ.
זמן לניסויים - חלק א'
תצטרכו את הדברים הבאים:- חופן של נגדים 10kΩ
- רב מודד
- מטריצה
בואו נעשה ניסוי פשוט כדי להוכיח שהדברים עובדים בדיוק כמו שתיארנו אותם.
קודם, נחבר כמה נגדי 10kΩ בטור ונראה איך הערכים שלהם מתווספים בצורה לא-מסתורית. נשתמש במטריצה, נכניס נגד 10kΩ אחד כמו שמתואר בתמונה הבאה ונמדוד את הערך שלו עם רב-מודד. טוב, אנחנו כבר יודעים שהוא יראה לנו 10kΩ, אבל זה מה שנקרא "בדיקת שפיות - sanity check". עכשיו כשאנחנו בטוחים שהעולם לא השתנה יותר מדי מאז שהסתכלנו עליו בפעם הקודמת, נכניס עוד נגד בצורה דומה, אבל כך שהרגליים של הנגדים יהיו מחוברות דרך המטריצה ונמדוד שוב. המודד צריך להראות לנו עכשיו ערך קרוב ל-20kΩ.
אתם עלולים לראות שההתנגדות שאתם מודדים לא בדיוק כמו שהנגד אומר שהיא צריכה להיות. לנגדים שונים יש רמת דיוק שונה, מה שאומר שהערך האמיתי שלהם יכול לסטות מהערך הרצוי בשני הכיוונים באחוז מסוים. כך שאתם יכולים לראות 9.99kΩ או 10.01kΩ. כל עוד הערך קרוב למה שהוא אמור להיות, הכל טוב.
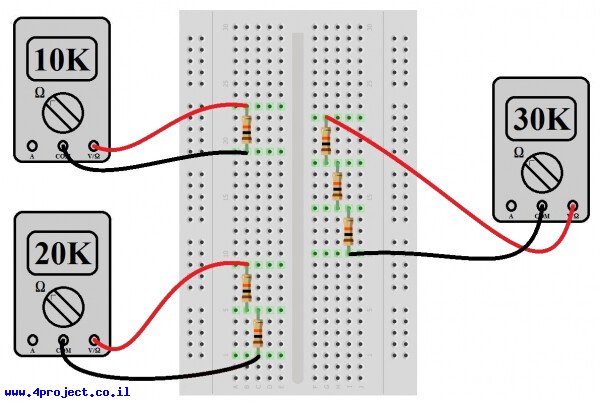
אתם יכולים להמשיך עם התרגיל הזה עד שתשתכנעו שאתם יודעים מה תהיה התוצאה של הוספת נגד נוסף, או עד שיגמרו לכם הנגדים, מה שיקרה קודם.
זמן לניסויים - חלק ב'
עכשיו בוא ננסה עם נגדים בחיבור מקבילי. תכניסו למטריצה נגד אחד של 10kΩ כמו קודם (אנחנו מאמינים שאתם כבר משוכנעים שמדידת ערך של נגד אחד יראה לנו משהו קרוב מאוד ל-10kΩ, כך שאין צורך לעשות את זה שוב). עכשיו תכניסו נגד נוסף כך ששתי הרגליים שלהם יהיו מחוברות חשמלית דרך שורות המטריצה. אבל לפני שתמדדו, תשתמשו באחת מהנוסחאות שהצגנו קודם, מה תהיה ההתנגדות הכוללת? (רמז: זה יהיה 5kΩ). עכשיו תמדדו. האם זה משהו קרוב ל-5kΩ? אם לא, בדקו שוב את החורים אליהם הכנסתם את הנגדים.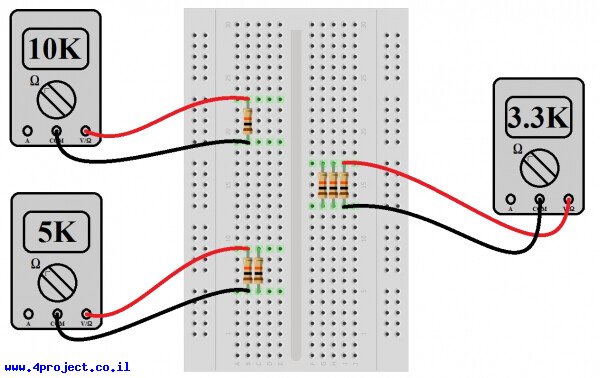
חזרו על התרגיל עם 3, 4 ו-5 נגדים. הערכים המחושבים/הנמדדים צריכים להיות 3.33kΩ, 2.5kΩ ו-2kΩ בהתאמה. האם הכל יצא כמו שתכננתם? אם לא, בדקו שוב את החיבורים. אם כן, כל הכבוד!
כללי אצבע לנגדים המחוברים בטור ובמקביל
יש מצבים שיידרשו שילוב יצירתי של נגדים. לדוגמה, אם אתם צריכים לייצר מתח ייחוס מאוד מסוים, כמעט תמיד תצטרכו יחס מאוד מסוים בין נגדים עם ערכים שהם כנראה לא ממש "סטנדרטיים". גם אם אפשר להשיג בשוק נגדים כמעט בכל ערך אפשרי, יכול להיות שלא תרצו לחכות X ימים עד שהמשלוח יגיע, או לשלם הרבה על ערכים לא כל כך פופולריים. אז תוך רגע תמיד אפשר לייצר ערך נגד משלך.טיפ מספר 1: נגדים זהים במקביל
חיבור N נגדים זהים בערך R מייצר לנו ערך של R/N. נניח שאתם צריכים נגד של 2.5kΩ, אבל יש לכם ארגז שלם של נגדי 10kΩ. חיבור של 4 מהם במקביל ייתן לכם 10kΩ/4 = 2.5kΩ.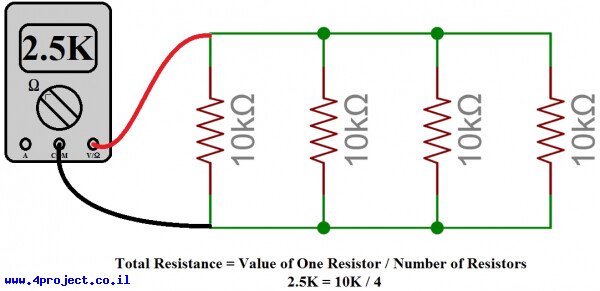
טיפ מספר 2: דיוק
דעו איזה דיוק אתם צריכים. לדוגמה, אם אתם צריכים נגד של 3.2kΩ, תוכלו להשתמש ב-3 נגדים של 10kΩ במקביל. תקבלו 3.33kΩ, שזה בערך 4% יותר ממה שצריך. אם המעגל שלכם דורש דיוק טוב יותר מ-4%, תוכלו למדוד את הערכים האמיתיים של נגדי ה-10kΩ שיש לכם כדי למצוא את אלה עם הערכים הנמוכים ביותר, מכיוון שלכל נגד גם כן יש דיוק מסוים. אם כל הנגדים שיש לכם הם בדיוק של 1%, אז אפשר להגיע רק ל-3.3kΩ. מכיוון שייצרנים עושים מדי פעם טעויות, לפעמים זה משתלם לבדוק טוב את מה שיש לכם בפועל.טיפ מספר 3: הגדרת הספק בחיבור טורי/מקבילי
שיטות חיבור אלה עוזרות גם לדירוג ההספק. נניח שאתם צריכים נגד של 100Ω מתאים להספק של 2W, אבל כל מה שיש לכם זה ערימה של נגדי 1kΩ להספק של 1/4W (והשעה כבר 3 בבוקר והקפה כבר קר…). תוכלו לחבר 10 נגדים כאלה במקביל כדי לקבל התנגדות של 100Ω (הרי 1kΩ/10 = 100Ω), וההספק הכולל יהיה 10x0.25W, או 2.5W. זה לא יראה יפה, אבל זה יקדם אתכם לסיום הפרוייקט ואולי תזכה אתכם בכמה נקודות בונוס על חשיבה יצירתית.צריך להיות קצת יותר זהירים כשמחברים במקביל נגדים עם ערכים והגדרות הספק שונות במקרים בהם יש חשיבות לערך הנגד הכולל ולהגדרת הספק.
טיפ מספר 4: נגדים שונים במקביל
ההתנגדות הכוללת של שני נגדים עם ערכים שונים תמיד תהיה קטנה יותר מההתנגדות של הנגד הקטן ביותר. אנשים רבים מחשבים את הערכים בראש ומגיעים לערך שהוא איפשהו בין שני ערכי הנגדים המחוברים במקביל (1kΩ || 10kΩ לא שווה איפה שהוא סביב 5kΩ!). ההתנגדות הכוללת תמיד תהיה קרוב יותר לערך הנגד הקטן (מלמטה). עשו לעצמכם טובה ותקראו את הטיפ מספר 4 לפחות 10 פעמים.טיפ מספר 5: פיזור הספק בחיבור מקבילי
פיזור ההספק בין נגדים מקביליים בערכים שונים לא מתפזר שווה בשווה בין הנגדים כי הזרמים לא שווים. אם נקח את הדוגמה הקודמת של 1kΩ || 10kΩ, אפשר לראות שהזרם שיעבור דרך נגד 1kΩ יהיה פי 10 גבוה יותר מהזרם דרך נגד 10kΩ.בסופו של דבר, הלקחים של הטיפים 4 ו-5 הם שצריך להקדיש יותר מחשבה ותשומת לב כשמשלבים נגדים שונים במקביל. טיפים 1 עד 3 מציעים כמה קיצורי דרך נוחים כשמדובר על נגדים זהים.
קבלים בחיבור טורי ומקבילי
שילוב קבלים זה כמו שילוב נגדים, רק להפך. עד כמה שזה נשמע מוזר, זה בדיוק כך. למה זה קורה?קבל מורכב משני לוחות קרובים אחד לשני, והתפקיד הבסיסי שלהם הוא להחזיק עליהם חבורה של אלקטרונים. כמה שערך הקיבול גדל, כך יותר אלקטרונים הם יכולים להחזיק. כשמגדילים את גודל הלוחות האלה, גדל גם ערך הקיבול, כי יש יותר שטח פיזי איפה שהאלקטרונים יכולים לבלות. ואם מרחיקים את הלוחות אחד מהשני, הקיבול יורד, כי השדה החשמלי ביניהם קטן כשהמרחק גדל.
בואו נגיד שיש לנו 2 קבלים של 10µF מחבורים בטור, ונגיד ששניהם טעונים.

זוכרים שבחיבור טורי לזרם יש רק מסלול אחד לזרימה? מכאן אפשר להסיק שכמות האלקטרונים שמשתחררים מהקבל התחתון תהיה זהה לאלקטרונים שיוצאים מהקבל העליון. אז הקיבול לא גדל, נכון?
למעשה, זה הרבה יותר גרוע מזה. ע"י חיבור הקבלים בטור אנחנו בעצם הרחקנו את הלוחות של הקבלים, כי בחיבור טורי המרחקים בין הלוחות מתווספים. אז אין לנו 20µF, וגם לא 10µF. במקרה זה יהיו לנו רק 5µF. התוצאה של זה היא שבחיבור טורי של קבלים אנחנו מחשבים את הערכים שלהם באותה הדרך בה אנחנו מחשבים את הערכים של הנגדים בחיבור מקבילי. גם הנוסחה המלאה וגם המקוצרת לשני נגדים מתאימה לקבלים.
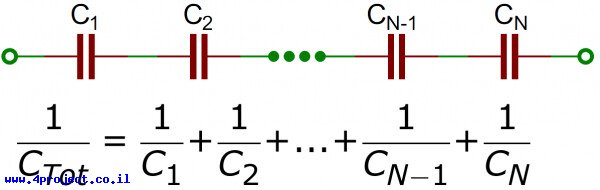
זה נראה כאילו שאין טעם לחבר קבלים בטור. צריך לציין שבמקרה כזה אנחנו מקבלים פי 2 מתח (או הגדרה של מתח מקסימלי). בדומה לסוללות, כשמחברים קבלים בטור, המתחים שלהם מתווספים.
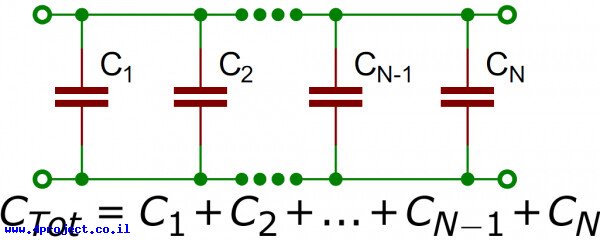
חיבור של קבלים במקביל דומה לחיבור הנגדים בטור: הערכים שלהם פשוט מתווספים אחד לשני. למה זה? החיבור במקביל למעשה מגדיל את גודל הלוחות של הקבל מבלי שהמרחק ביניהם גדל. שטח גדול יותר שווה לקיבול גדול יותר. פשוט מאוד.
זמן לניסויים - חלק ג'
תצטרכו את הדברים הבאים:בואו נראה חיבור טורי ומקבילי של קבלים בפעולה. זה יהיה קצת יותר מסובך מהתרגיל עם הנגדים, כי קשה יותר למדוד קיבול ישירות עם רב מודד.
קודם נדבר על מה שקורה כשהקבל נטען. הזרם מתחיל להיכנס דרך אחד החיבורים, כמות זהה של זרם יוצא מהחיבור השני. ואם אין שום התנגדות בטור לקבל, זה יכול להיות די הרבה זרם. בכל מקרה, הזרם זורם עד שהקבל נטען עד למתח שחיברנו, בזמן זה הזרם פוחת, עד לנקודה בה המתח בקבל שווה למתח האספקה, אז הזרם נפסק לחלוטין.
כמו שאמרנו קודם, הזרם יכול להיות די גדול אם אין נגד בטור לקבל, והזמן עד לטעינה מלאה יכול להיות מאוד קצר (סדרי גודל של מילישניות או אפילו פחות). לצורך הניסוי, אנחנו רוצים להיות מסוגלים לראות איך הקבל נטען, כך שנשתמש בנגד של 10kΩ בטור כדי להאט את התהליך לרמה שנוכל לראות אותו בקלות. אבל קודם צריך להסביר מהו קבוע זמן RC.
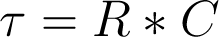
מה שהנוסחה הזו אומרת היא שקבוע הזמן בשניות (שנקרא tau) שווה להתנגדות באוהמים כפול קיבול בפאראד. פשוט? לא? נדגים את זה בהמשך.
זמן לניסויים - חלק ג', המשך…
לחלק הראשון של הניסוי נשתמש בנגד אחד של 10kΩ וקבל אחד של 100µF (ששווה ל-0.0001 פאראד). שני רכיבים אלה מייצרים קבוע זמן של שניה אחת: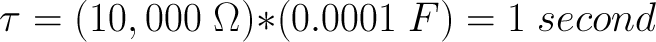
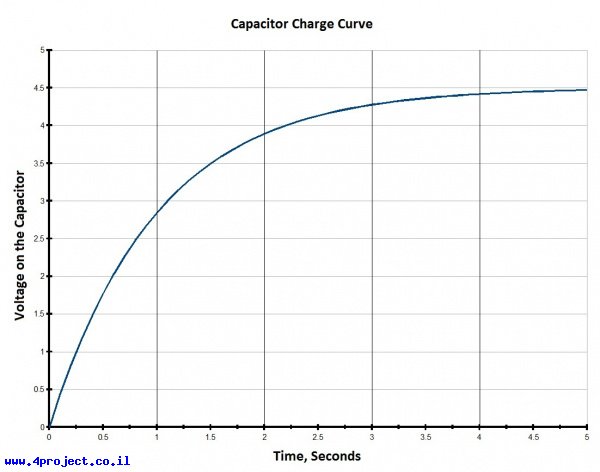
כשטוענים את הקבל של 100µF דרך נגד של 10kΩ, אנחנו מצפים שמתח על הקבל יעלה לכ-63% ממתח האספקה תוך קבוע זמן אחד, שהוא שניה אחת. אחרי 5 קבועי זמן (5 שניות במקרה הזה), הקבל יהיה טעון ל-99% ממתח האספקה וגרף הטעינה יראה דומה לשרטוט הזה:
עכשיו, כשאנחנו יודעים את הדברים האלה, נחבר את המעגל לפי התמונה הבאה (שימו לב שחיברתם את קוטביות הקבל בצורה הנכונה!).
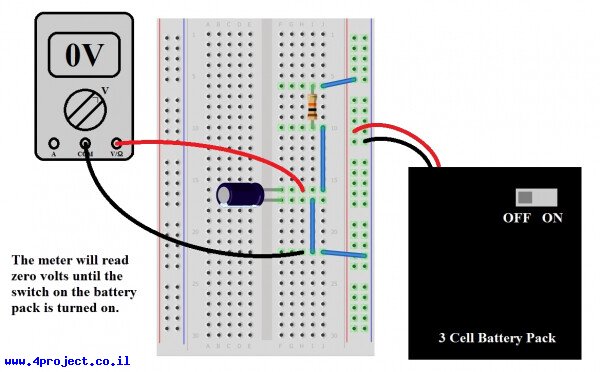
עם רב מודד מכוון למצב מדידת מתח, בדקו את מתח הסוללות כאשר המפסק שלהם דלוק (ON). זהו מתח האספקה שלנו, והוא אמור להיות סביב 4.5V (יכול להיות קצת יותר אם הסוללות חדשות). עכשיו חברו את המעגל, כבו את המפסק של הסוללות (OFF) לפני שאתם מחברים אותם למטריצה. בנוסף, שימו לב שהחוט האדום והשחור הולכים למקומות הנכונים. אם זה יותר נוח, תוכלו להשתמש בחוטי תנין כדי לחבר פרובים (חוטים) של הרב מודד לרגלי הקבל כדי למדוד בצורה קבועה (רצוי גם להרחיב את הרגליים של הקבל כדי שיהיה יותר קל).
כשתהיו מרוצים והמעגל יראה תקין, כוונו את הרב מודד לתצוגת מתח, תזיזו את המפסק של בית הסוללות ל-"ON". לאחר כ-5 שניות, רב מודד אמור להראות מתח די דומה למתח הסוללות, מה שמראה שהנוסחה נכונה ואתם יודעים מה אתם עושים. עכשיו כבו את המפסק ל-OFF. המתח עדיין נשמר פחות או יותר, נכון? זה בגלל שלזרם אין מסלול דרכו הוא יוכל לפרוק את הקבל, יש לנו מעגל פתוח. כדי לפרוק את הקבל תוכלו להשתמש בנגד 10K נוסף במקביל לקבל. אחרי כ-5 שניות המתח יירד די קרוב ל-0.
זמן לניסויים - חלק ג', עוד קצת…
הגענו לחלק המעניין. נתחיל עם חיבור שני קבלים בטור. זוכרים שאמרנו שהתוצאה תהיה כמו חיבור של שני נגדים במקביל? אם זה נכון, נצפה שהקיבול יקטן בחצי: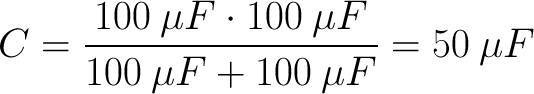
ומה זה יעשה לקבוע הזמן שלנו?
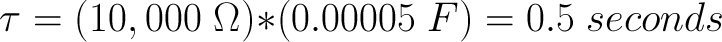
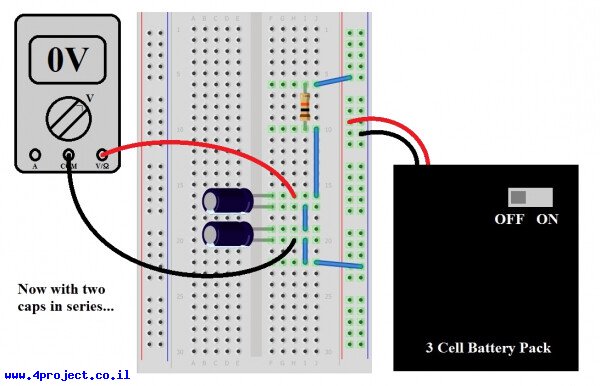
חברו קבל נוסף בטור לזה שכבר חיברתם, וודאו שרב מודד מראה 0 וולט (או משהו באיזור זה) והזיזו את מפסק הסוללות ל-ON. האם לקח בערך חצי מהזמן להיטען למתח הסוללות? זה בגלל שיש לנו רק חצי מהקיבול שהיה. מיכל הדלק של האלקטרונים נהיה קטן יותר, כך שזה לוקח פחות זמן למלא אותו. קבל שלישי שהמלצנו לניסוי זה הוא רק כדי להוכיח את הנקודה, אבל אנחנו מאמינים שהבנתם את הכיוון.
עכשיו בואו ננסה קבלים בחיבור מקבילי. אמרנו קודם שזה יהיה כמו חיבור של שני נגדים בטור. אם זה נכון, אז אנחנו צריכים לצפות לקיבול של 200µF, נכון? אז קבוע הזמן שלנו יהיה:

זה אומר שעכשיו יקח כ-10 שניות עד שהקבלים המקביליים יטענו למתח של 4.5V שמסופק להם.
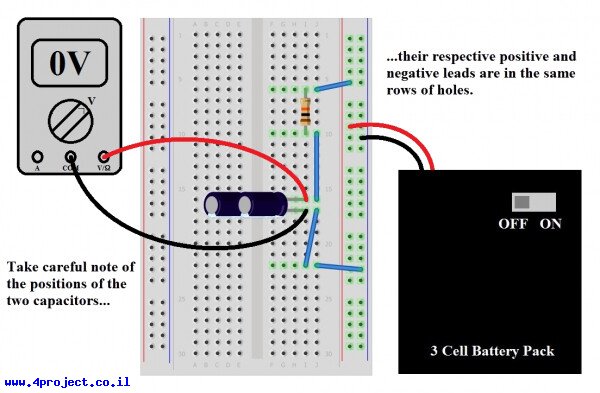
לצורך ההוכחה, תתחילו עם הניסוי המקורי עם נגד אחד של 10kΩ וקבל אחד של 100µF בטור, כמו שחיברנו בניסוי הראשון. אנחנו כבר יודעים שלוקח לקבל להיטען כ-5 שניות. תוסיפו את הקבל השני במקביל. וודאו שרב מודד מראה 0 וולט (פרקו את הקבל דרך נגד אם זה לא מראה 0), תדליקו את הסוללות. לוקח יותר זמן, נכון? ברור, הגדלנו את מיכל הדלק של האלקטרונים ועכשיו לוקח יותר זמן למלא אותו. כדי להוכיח את הנקודה לעצמכם, חברו קבל שלישי של 100µF במקביל ועקבו אחרי הטעינה, שלוקחת די הרבה זמן.
סלילים בחיבור טורי ומקבילי
מקרים בהם צריך לחבר סלילים בטור או במקביל הם די נדירים, אבל יכולים לקרות. בכל מקרה בואו נכסה גם את המקרים האלה.בקצרה, הערכים שלהם מתווספים בדיוק כמו של הנגדים, מסכמים את הערכים כשהם מחוברים בטור ואת ההפכים שלהם כשמחוברים במקביל. החלק הטריקי הוא שכהסלילים ממוקמים קרוב אחד לשני, אז השדות המגנטיים שלהם משפיעים אחד על השני, אם זה בכוונה או לא. זו הסיבה שרצוי שיהיה סליל אחד במעגל ולא שתיים או יותר, אם כי רוב הסלילים מוגנים כדי למנוע מקרים כאלה.
בכל מקרה, מספיק לומר שהערכים שלהם מתווספים כמו של הנגדים. מידע נוסף על נושא זה הוא הרבה מעבר למדריך זה.
לאן ממשיכים?
עכשיו כשאתם מכירים את היסודות של מעגלים טוריים ומקביליים, למה שלא תבדקו גם את המדריכים הבאים?- מחלקי מתח - אחד המעגלים הבסיסיים וכאלה שחוזרים על עצמם הם מחלקי מתח. זהו מעגל שכולו בנוי על הנושא שלמדנו במדריך זה
- מהו ארדואינו - יש לכם כבר הבנה טובה במעגלים בסיסיים, תוכלו להתחיל ללמוד על מיקרובקרים עם אחד הכרטיסים הפופולריים ביותר - Arduino
- כפתורים ומפסקים - הזכרנו כמה מרכיבי המעגל הבסיסיים במדריך זה, אבל לא את אלה. מפסקים הם רכיב קריטי כמעט בכל פרוייקט. תלמדו הכל על המפסקים במדריך זה
- תפירה עם חוט מוליך (TODO - Sewing with Conductive Thread) - מעגלים לא חייבים להיות מורכבים רק ממטריצה וחוטי גישור. בתחום ה-E-textile (אלקטרוניקה לבישה) משתמשים בחוט תפירה מוליך כדי לתפור מנורות ורכיבי אלקטרוניקה אחרים לתוך בגדים או מוצרים אחרים.